|
 Quadratics Practice 2016
Six questions, of progressive difficulty, each on 'complete the square then solve', 'factorise then solve', 'quadratic formula to solve'. PDF here.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Four Circles
Not much info on this diagram but can you find the equation of the small blue circle? Includes Answers. PDF here.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Quadratic Formula Synthesis
Complete the steps in the table to get from ax2+bx+c=0 to the quadratic formula. Or, cut out the steps and ask students to arrange them in the correct order. Answers on page 1, empty table on page 2, the peices in a random order on page 3. PDF here
|
|
|
|
Max Box
What's the biggest area you can contain with x cm of string? Whats the biggest volume you can contain with an A4 sheet of paper? Not as easy as it seems! Our answers and Autograph file used.
|
|
|
|
|
|
|
|
|
|
|
|
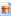 A Level Formulae
A lovely spider diagram jpeg noting all the useful formulas required for A Level Mathematics. Print out, explore, learn.
|
|
|
|
Key Pairs
Interactive match up pairs starter activity for key elements of A level maths basics, great for revision.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Factorising Polynomials
Use combinations of the factors given to make the polynomials. An easier and harder version with answers included for both. Pdf here.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Graph Transformations
Kinesthetic activity for students. PDF here. Print out the graphs onto A4 paper, then print the final 6 slides onto accetate and cut up. Pupils use the accetates to show the required graph transformations. Smaller print version, this one prints all the original graphs onto 2 A4 sides, another page on tracing paper for the graphs. PDF of this file here.
|
|
|
|
Compound Transformations
Students use the equations given, together with some of thier own creation, to match to the written transformations. Extension questions too on order of transformations.
|
|
|
|
Trigonometry Recap
Four questions based on each of; Pythagoras, standard right-angled trig, sine rule, cosine rule and sine rule for area. Answers included. PDF here.
|
|
|
|
|
|
|
|
APs & GPs
Notes on A Level APs & GPs (Arithmetic Progressions & Geometric Progressions). PDF here
|
|
|
|
|
|
|
|
Series Questions
Questions and extensions based on an A level exam question involving sums of both arithmetic and geometric series. Includes answers. PDF here.
|
|
|
|
|
|
|
|
 Introducing Exponentials
A few quick starter questions on solving exponential and log equations as well as differentiating and integrating them. Includes Answers. PDF here.
|
|
|
|
Binomial Activity
Four different introductions to the binomial expansion. Spread around class, complete, and then present to other students. An activity to really reinforce the imprortance of the binomial expansion across several areas of Mathematics. PDF here.
|
|
|
|
Binomial Expansions
A progression of binomial expansions to take students from the very straightforward (x+1)3 to (3-2x)5 in easy steps.
|
|
|
|
Binomial Expansion Concept Questions
A couple of questions to highlight finding all terms vs using binomial formula to find just one term. Contains an easier and harder question, with answers.
|
|
|
|
Making Progress Revision Notes
All of the required formulae for the old AQA Core 2 module on a single side of A4. Arranged into those formula that must be remembered and those that are, or were, given in the formula book. Tested and much appreciated by my sixth form class!
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Confusing Transformations
Describe the geometrical transformations of the graphs, building up from easier to more complicated compound transformations. Includes answers. PDF here.
|
|
|
|
|
|
|
|
|
|
|
|
Chain, Product, Quotient Tough Recap
A set each of chain rule, product rule and quotient rule questions. Each set including easy, medium and hard questions (the rows) and polynomial, trigonometrical and exponential questions (the columns). My Yr13 students (single and further maths) really enjoyed recapping their knowledge with this task!
Answers included. As PDF version.
|
|
|
|
Methods for Integration
Info sheet on identifying aspects to look for when deciding which method for integration, followed by six (mostly exam) questions to practise each method. Includes answers. As pdf here.
|
|
|
|
|
|
|
|
Integration - Choose Your Method
Here's a whole bunch of integration questions for you to decide how to integrate. These cover all methods including by substitution, by parts, by partial fractions etc. Some interesting limits for you to work your way through too. There is some structure to the layout of the questions on this document but we'll leave you to work out what that structure is! Includes answers. As pdf here.
|
|
|
|
Integrate These
Another selection of good integration questions to test your skills. Includes answers. As pdf here.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Embedded Within
A template for students to create their own chain, product, quotient questions where chain, product or quotient rule is used within the whole question also of the format, chain, product, quotient. PDF here.
|
|
|
|
The Chain Rule
Nine questions of progressive difficulty for students to develop 'a rule' for differentiating y other methods than brute force expanding out.
|
|
|
|
Chain Rule Practice
Set of questions of progressive difficulty for students to familiarise themselves with the chain rule, answers included. PDF here
|
|
|
|
|
|
|
|
Chain Rule, Product Rule, Quotient Rule Matchup Exercises
Three sets, each of three matchup puzzles, for pupils to practice chain rule, product rule and quotient rule. Answers included together with blank templates for pupils to create their own puzzles. PDFs here, here and here.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Functions Activity
A matchup cards activity to check & consolidate understanding of domain vs range and mapping.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Proving Trig Identities
Prove the trigonometric identities by matching up the peices (steps) in the correct order. Supports students with this topic by providing the steps , and avoiding alebraic mistakes that confuse the key learning outcomes, whilst challenging them to understand the order and making connections between each step. PDF here
|
|
|
|
|
|
|
|
Harmonic Form
The formula, or format, followed by a teaching activity and proof on the next page. PDF here.
|
|
|
|
Partial Fractions
The partial fractions formulae in big, to save writing it out. Plus a explanation of the various formats of partial fractions, such as when they include whole terms Ax + B etc. PDF here.
|
|
|
|
Binomial Theorem
The formula plus 8 questions to practice (answers on the second page), and teaching ideas on the third page. Pdf version.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Vectors to Resolve Forces
Dynamic Autograph file for demonstrating how vectors can be added and how to find the magnitude of a vector.
|
|
|
|
|
|
|
|
|
|
|
